最近工作需要，又重温了一下电路知识，对拉氏变换有了“新”的理解。

众所周知，高斯小时候就原创了求和公式。求和公式就是将大量的加法运算变成了简单的乘法。换个思路看，天地自然宽。

电路中很多微积分方程，如何解就很烦人。我们能否换一个工作域，将微积分变成我们熟悉的乘除法呢？

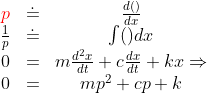
翻开数学工具箱，复数看着靠谱。复数有三种表达方式，欧拉公式将其转成简单的指数表达方式：

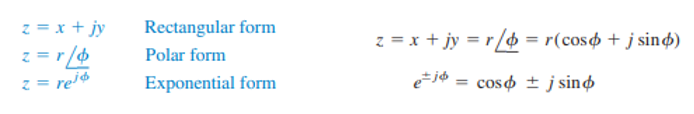
不去管复数的具体含义，运算从实数转成复数后，乘除法变成了加减法，微积分变成乘除法

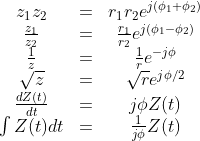
数转为复数域，那么函数呢？从上面我们看到指数很有用。哪个积分变换用到了指数呢？大名鼎鼎的傅里叶变换啊。不负众望，时域的微积分变成了频域的乘除法。

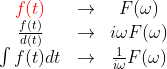
傅里叶变换有一个小问题，要求函数绝对可积，也就是积分是要有限的，否则搞出来都是无穷就没有意义了。但是电路中很多函数不满足这个条件，比如x^{2。那怎么办呢？}

拉普拉斯跳出来说，我可以把他变小啊。指数是增长/衰减最快的了。不管你函数多大，我给你乘上一个衰减因子e^{-at，在t足够大的时候，都能给你拉下来，满足傅里叶条件了。}

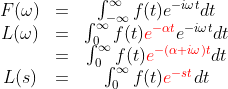
指数相乘可以合并为加法，a+jw不就是一个复数s吗？这样就成了大名鼎鼎的拉氏变换了。

有了这些数学工具，我们可以将电路中的各种变量变成复数，方程转到复频域，这样微积分就变成了我们熟悉的多项式。做完操作再用逆拉普拉斯变换转回来就好了。